ÁREA DE UN CUERPO GEOMÉTRICO
El área es la medida de una región interior, entonces, para obtener el área de cualquier poliedro deberemos calcular la medida de todas sus caras.
Figura
|
Esquema
|
Área
|
Volumen
|
| Cilindro | 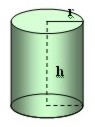 | ||
| Esfera | 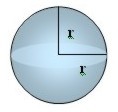 | ||
| Cono | 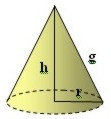 | ||
| Cubo | 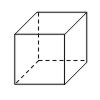 |
A = 6 a2
|
V = a3
|
| Prisma | 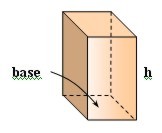 |
A = (perim. base • h) + 2 • area base
|
V = área base • h
|
| Pirámide | 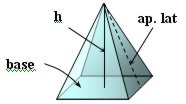 |
Poliedros regulares
Figura
|
Esquema
|
Nº de caras
|
Área
|
| Tetraedro | 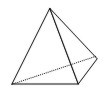 | 4 caras, triángulos equiláteros | |
| Octaedro | 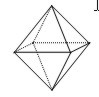 | 8 caras, triángulos equiláteros | |
| Cubo |  | 6 caras, cuadrados | A = 6 a2 |
| Dodecaedro | 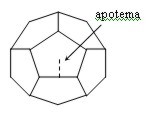 | 12 caras, pentágonos regulares | A = 30 · a · ap. |
| Icosaedro | 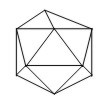 | 20 caras, triángulos equiláteros |
VOLÚMENES DE CUERPOS GEOMÉTRICOS.
El volumen de un cuerpo es la cantidad de espacio que ocupa. La unidad principal es el metro cúbico (m3).

VÍDEO